1. 介绍

如今AlphaGo的名字已是家喻户晓，它是人工智能领域的非常重要的里程碑事件。我们知道，围棋的特征空间高达361！个，以至于目前的计算力在有限的时间内根本无法完成搜索。本文从纯技术角度聊一聊AlphaGo是如何解决该问题的，探究一下它成功的原因和技术细节。本文大部分细节来自于Deepmind在Nature的论文《Mastering the game of Go with deep neural networks and tree search》。
AlphaGo技术点主要分为3大部分：策略网络(Policy Network)、价值网络(Value Network)、蒙特卡洛树搜索(MCTS)。然后采用离线训练+在线博弈的方式，将三种技术结合起来，最终出”棋“致胜。

2. 离线训练技术

本节将介绍AlphaGo中的4种离线训练的网络结构，这些训练好的网络将会被应用于围棋的在线博弈中。

2.1 监督学习策略网络(SL Policy Network)

AlphaGo基于3万多人类围棋专家的棋谱，采用监督学习的方式训练了一个13层的Deep Q Network(DQN)，称为SL Policy Network，$p_\sigma$，实现了end-to-end的预测。DQN采用经验回放和target network更新两种方式解决了强化学习中非线性拟合（如神经网络）不收敛的问题。

SL Policy Net的输入是围棋19*19像素图片和一些人工定义的围棋先验知识，输出是当前特征下每个合理动作的概率$p_\sigma(a|s)$，目标最大化似然函数$logp_\sigma (a|s)$，更新方式是梯度上升。

SL Policy的优点是准确率较高，缺点是走子速度相对较慢：基于全部特征的SL Policy准确率达到了57.0%，基于棋盘信息和下棋历史信息的SL Policy准确率达到了55.7%，走一步需要大约3ms。

2.2 快速走子网络(Fast Rollout Policy Network)

跟SL Policy Network类似，AlphaGo基于3万多人类围棋专家的棋谱又训练了一个Fast Rollout Policy，$p_\pi$。Fast Rollout Policy与SL Policy的输出完全相同，不同的是Rollout Policy使用了更少的特征和特征的线性组合，牺牲了一定精度换取了更快的走子速度。Rollout Policy的准确率约为24.29%，走子速度约为2$\mu s$。 Rollout Policy主要用于MCTS，快速走子来估计局面。

2.3 强化学习网络(Reinforcement Learning Policy Network)

当基于先验知识的SL Policy Network训练好之后，AlphaGo已经拥有人类专家的平均水平了。在此基础上，AlphaGo采用基于策略梯度的强化学习自我对弈的方式做进一步提升，称之为RL Policy Network，$p_\rho$。RL Policy Network的网络结构与SL Policy Network一样，它的参数初始权重$\rho$使用训练好了的SL Policy的参数权重$\sigma$。

对弈过程中，用几回合之前的RL Policy Net和最新RL Policy Net对弈。首先随机行成一个对局的开局，然后从该时刻$t=t_0$开始博弈直到游戏结束$t=t_T$。设置胜方$reward(t_T) = 1$，败方$reward(t_T) = -1$，然后对胜负棋局分别用最大似然更新每一步：$$\sum_{s_t} logp_\sigma (a_t|s_t)reward(t)$$

2.4 价值网络(Value Network)

Value Network$V^p(s)$用来给当前局面”打分“，即所谓的大局观。Value Network的结构跟RL Policy Net基本一样，只是最后一层的输出由概率分布变成了单个值。
Value Network基于以下步骤自我博弈生成了3000万个对局信息：

  1. 随机生成一个数字 $U \sim N(1, 450)$;
  2. 用SL policy network $a_t \sim p_\sigma(·|s_t)$生成前U−1步局面;
  3. 第U步随机选择$a_u ~ unif{1, 361}$，但必须符合围棋规则;
  4. 从第U+1步开始，使用RL Policy Net$a_t \sim p_\rho(·|s_t)$博弈直到游戏结束，得到游戏结果$reward(t_T)$；
  5. 将$(S_{U+1},reward_{U+1})$加入样本池中，用于后续Value Network训练的训练。

注意：第1、2、3步增加了样本的多样性；损失函数是MSE。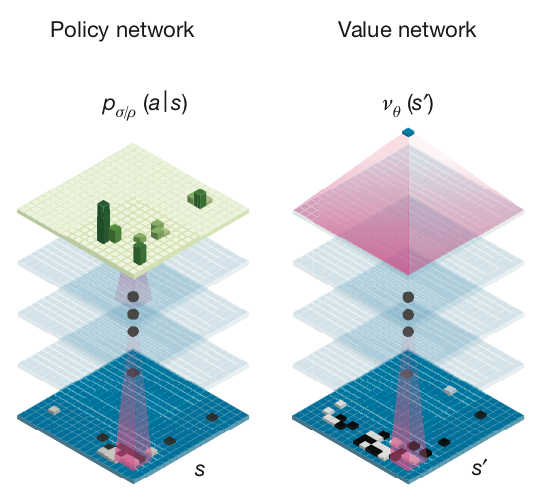
ac algorithm

3. 在线博弈

在线博弈主要将MCTS与训练好的网络相结合，基于当前局面做出最优的动作选择。

3.1 蒙特卡洛书搜索(MCTS)

MCTS是一种用于博弈游戏寻找最优解决方案的算法。MCTS会基于当前局面做多次模拟博弈，并尝试根据模拟结果预测最优的移动方案。AlphaGo中的MCTS进行一次模拟有以下4步：

  1. Selection：在当前局面，根据UCB1算法选择回报值最高的动作：$$a_t = argmax(Q(s_t,a)+\mu(s_t,a)),\quad \mu \propto \frac{P(s,a)}{1+N(s,a)}$$重复选择L步到达一个叶子节点$s_L$。
  2. Expansion：利用SL Policy Network，$p_\sigma$的将叶节点$s_L$扩展，并将输出的概率分布作为先验概率$P(s,a)=p_{\sigma}(a|s)$存下来。
  3. Evaluation：评估叶节点$s_L$。采用价值网络进行估值$v_\theta(s_L)$，并采用Rollout Policy $p_\pi$博弈直到游戏结束，获得回报$z_L$。
  4. Backup：更新蒙特卡洛树。$$\begin{equation}\begin{split}
    V(s_L) &= (1 - \lambda)v_\theta(s_L) + \lambda z_L\\
    N(s,a) &= \sum^n_{i=1}1(s,a,i)\\
    Q(s,a) &= \frac{1}{N(s,a)}\sum^n_{i=1}1(s,a,i)V(s^i_L)
    \end{split}\end{equation}$$其中$s^i_L$是第i次模拟的叶子节点；$1(s,a,i)$表示(s,a)在第i次模拟是否被访问。当模拟结束，算法会选择访问最多次的动作作为预测动作。

下图是AlphaGo Nature论文中对MCTS的总结：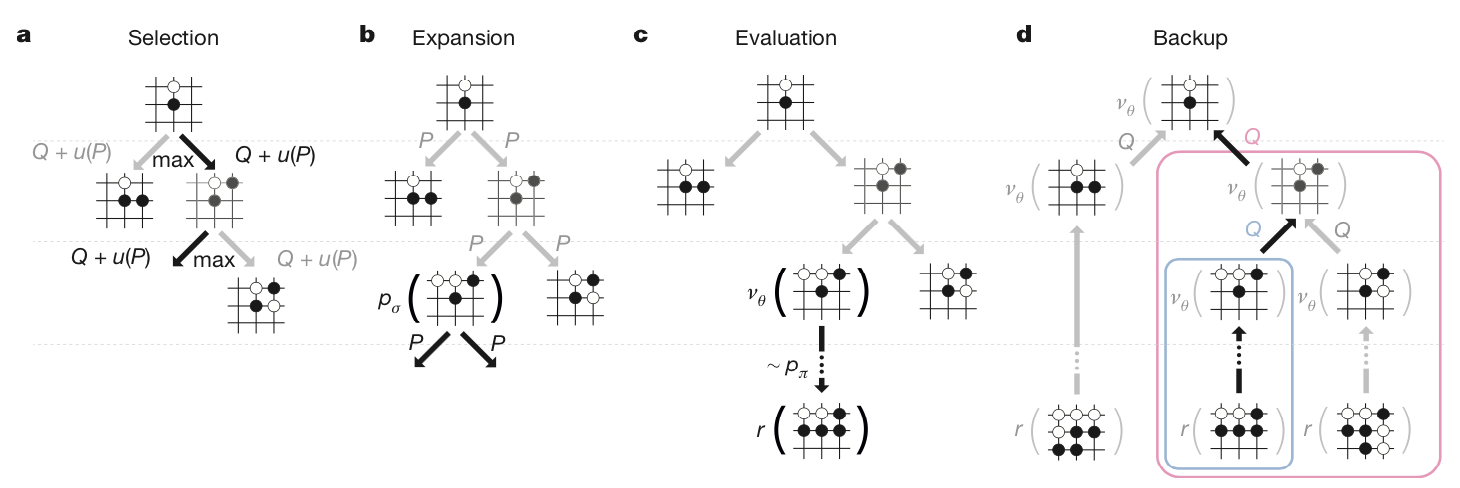
ac algorithm

4. 结果模拟

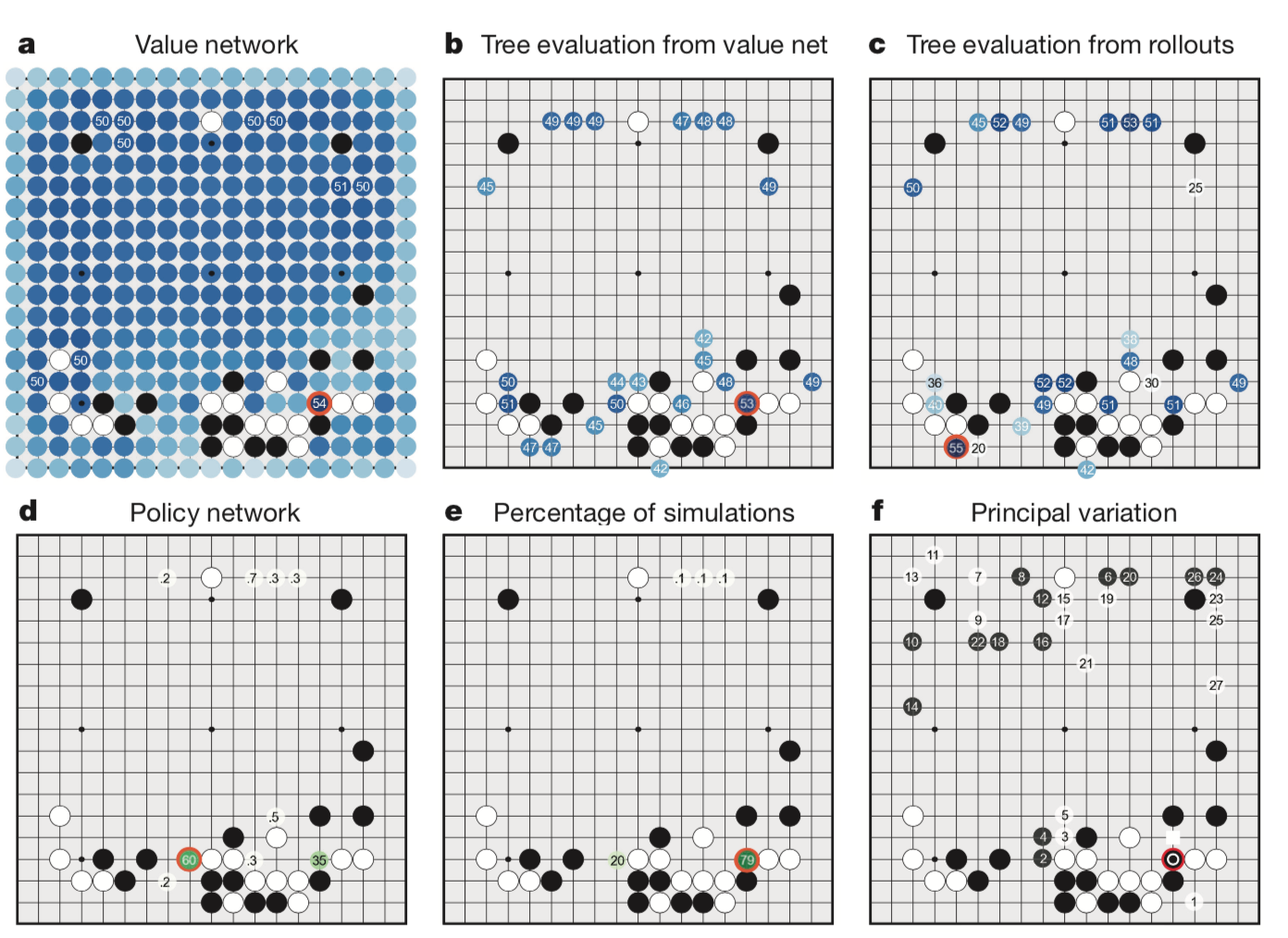
ac algorithm

a. 基于当前局面，value network $v_\theta(s’)$对所有的候选位置的评估。
b. 仅用value network$v_\theta(s’)$做评估，多次模拟后得到平均Q(s,a)。(即$\lambda = 0$)
c. 仅用rollouts network$v_\pi(s,a)$做评估，多次模拟后得到平均Q(s,a)。(即$\lambda = 1$)。
d. 根据SL policy network $P_\sigma(a|s)$选择的动作概率（大于0.1%）